My approach to ecosystemic programming has involved conceptualizing the final product as a physically navigable space, as a metaphoric sculptural mobile (audible-mobile) or as an orrery (a mechanical model of the solar system).  Thinking about the behavior of sound in a physical space with these metaphoric models enables me to visualize the results of my programming in a fairly intuitive way. In each of these models, I consider the different sonic elements (Kyma Sounds) of a musical ecosystem as equivalent to the independent physical objects constituting a kinetic sculpture, mobile, or orrery. The objects/Sounds may be programmed to move within and interact with their environment with some degree of agency, or be fixed in their behavior, functioning as fixed points of reference for other objects to respond to.

At the Hirschhorn Museum in Washington, D.C., I first encountered the Alexander Calder mobile pictured above when entering this curving hallway. It was free to move and reorient itself, but had found a kind of balance in the environment of the hallway at that moment. There was potential for motion, but if it was happening, it was at a very slow pace. I was intrigued by the sculpture, volumes and colors in space, connected to each other and the surrounding environment, creating a tension between the potential for movement and the status quo of its position. I repositioned myself in the environment, and my new perspective revealed more about the sculpture, its constituent parts, and their relationships to each other.

As the sonic ecosystem unfolds for the performer(s) and/or audience, the individual objects adopt a perceptually different relationship to other objects and the environment as a whole. Their motion in space, especially when coupled with spectral transformation, reveals aspects of the larger structure and various individual objects that we might otherwise not perceive. Now the metaphor of sculpture/mobile/orrery assumes the role of guiding our perception of musical structure.

I believe this process of revelation influences how we choose to interact with the sonic environment we find ourselves a part of, guiding performer behavior and listener appreciation, perhaps assuming an educational role, certainly providing a framework for experiencing the sonic art.

(N.B. For the following examples, use the following Speaker Setup in the Preferences: Quad, no sub; or equidistant Eight Channel. Download the examples here: Ecosystemic Programming Part 2.kym )

In Part 1, I left off with stereo panning managed by amplitude feedback, and it is a simple matter to scale this up to multichannel output. This will create objects that move independently in space on the horizontal plane (panning) throughout the entire sonic environment, responding to localized changes of amplitude. The source of those changes may be other objects in the environment generated by Kyma, external (e.g. human) performers, or the object itself. The objects may be programmed to fully circumnavigate the multichannel output, or constrained to a portion of it.

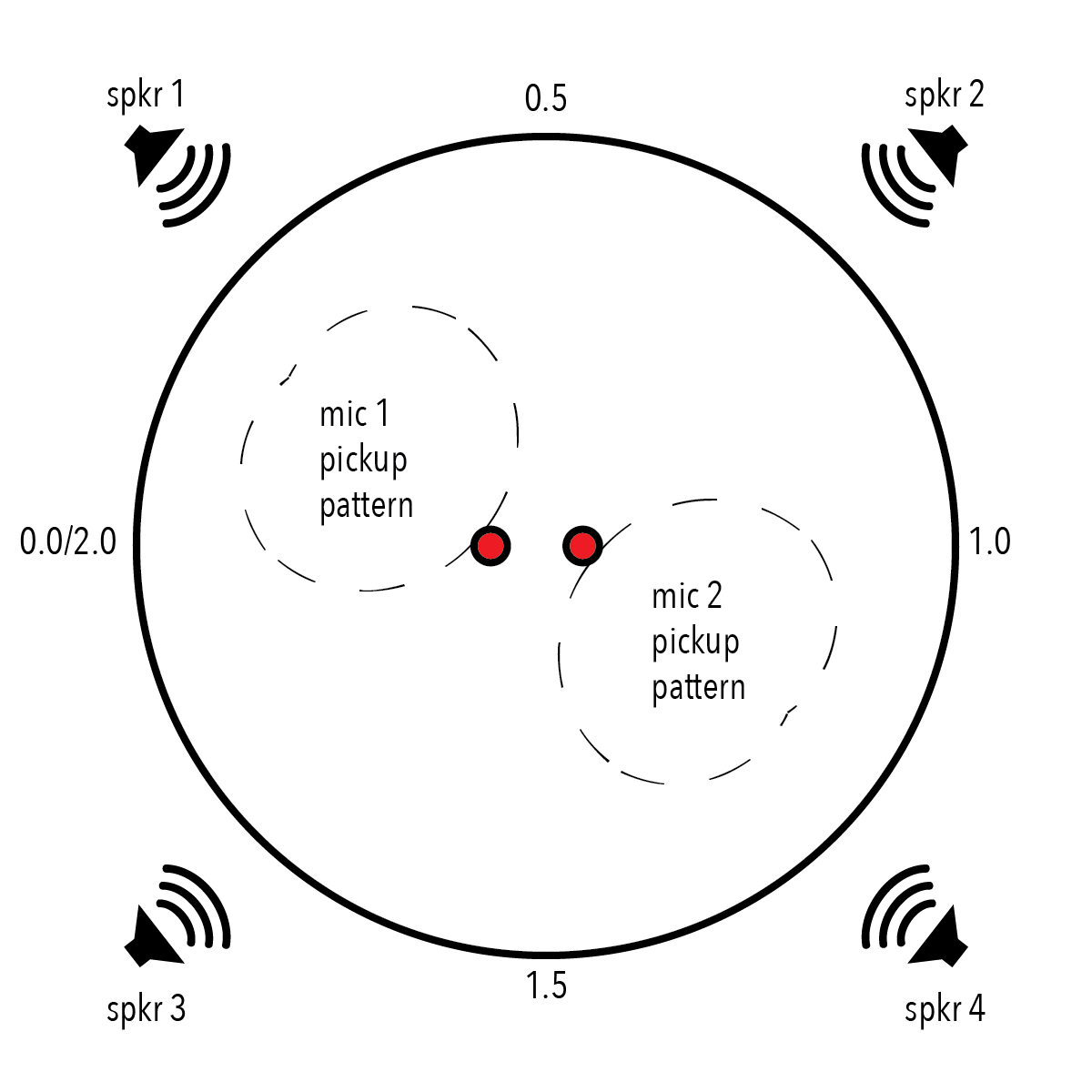
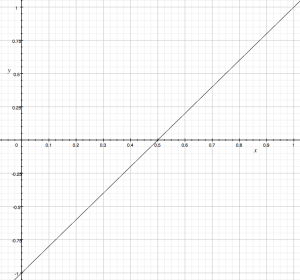
In the Stereo Amp Panning sound, the value for !Angle ranges from 0 to 1 (0,1). Scaling up the output for multichannel will enable the full range of surround panning if the range of values is ≥ 2. This can be achieved simply by multiplying the value for !Angle. Figure 1 shows a quadraphonic arrangement of speakers with two cardioid microphones, a basic arrangement for the presentation of ecosystemic work. The numbered circle represents the field of sound perceived with a fixed !Radius of 1 and a variable !Angle. !Angle 0.0 is hard left, 0.5 center, and 1.0 hard right, presenting the range of possible angles in a stereo setup. In the quadraphonic arrangement, values greater than 1 will continue clockwise around the arc, until 2.0, which is perceptually the same as 0.0. If we were to continue beyond 2.0, the source of the sound would continue to move clockwise, around and around.  In an ecosystemic environment, scaling the output of !Angle to some number much greater than 2 has the effect of magnifying the responsiveness of the object to changes in its environment.

Decreasing the value of !Angle creates the perception of counterclockwise motion towards 0.0. Negative !Angle values are valid, and decreasing the value below 0.0 continues the perceived motion, again, ad infinitum. see Figure 2

In the quadraphonic environment described in figures 1 and 2, an increase of output from speaker 1 will be detected by microphone 1 most clearly. If this input is selected for amplitude tracking and generates a value for !Angle, the sound it is a part of will move clockwise away from speaker 1 (!Angle value 0.25). As this behavior reduces the output of speaker 1, and therefore the value of !Angle, the sound will move counterclockwise toward the speaker, until again repelled by the output of speaker 1.

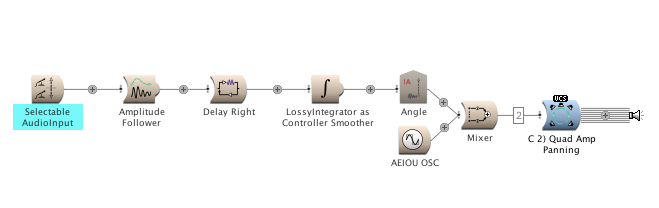
The Sound C 2) Quad Amp Panning is the same as B) Stereo Amp Panning, with the addition of a MultichannelPan output.

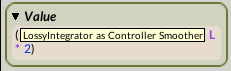
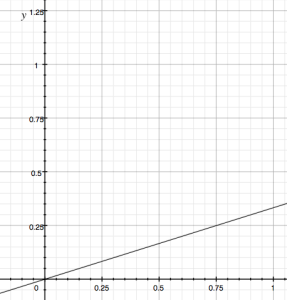
The data entering SoundToGlobalController (from the LossyIntegrator) is scaled by 2, in order to produce a value for !Angle ranging from 0 to 2 (0,2).

  

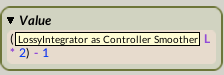
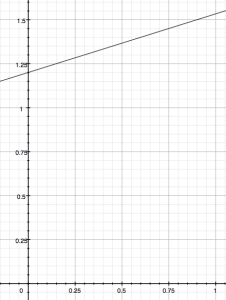
Offsetting the data by the addition or subtraction of some amount allows us to manage the range of values. Perceptually, where !Angle is concerned, offsetting determines the starting/resting/centering position of the sound before it moves. Common approaches to offsetting !Angle include subtracting 1 from the value, resulting in a range of (-1, 1):

  

and its opposite:

  

It may be desirable to constrain the possible values for !Angle by scaling down, rather than up, in order to limit the range of motion. Multiplying by less than 1 produces a scale limited range.

  

And in the following case, combining a scaled down value and offsetting it results in the sound beginning in the Left Surround speaker (speaker 4)  of a quadraphonic system and having a range of motion limited to about 60º. If this value is generated from audio captured by microphone 1 in the quadraphonic setup of figures 1 and 2, it would likely rest at the offset position unless another sound source were introduced that mic 1 would be sensitive to. Changing the input to microphone 2 would result in more panning activity.

  

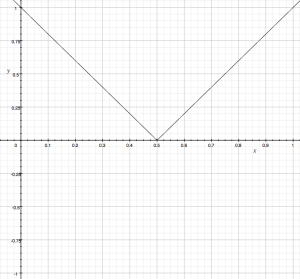
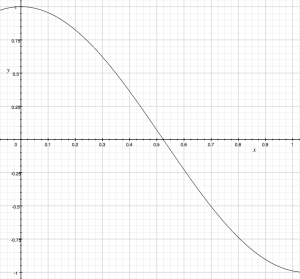
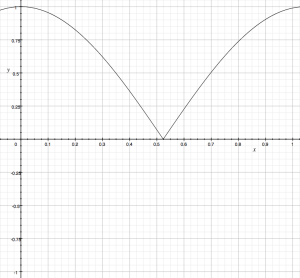
So far, the examples have all been linear mappings of the audio data to generate the !Angle of the sound. Very simple (and sometimes complex) modifications to the algorithms can produce interesting non-linear mappings. For example, if we take absolute value of the scaled and offset ((x*2) – 1),

it results in a flipped positive triangle mapping.

     

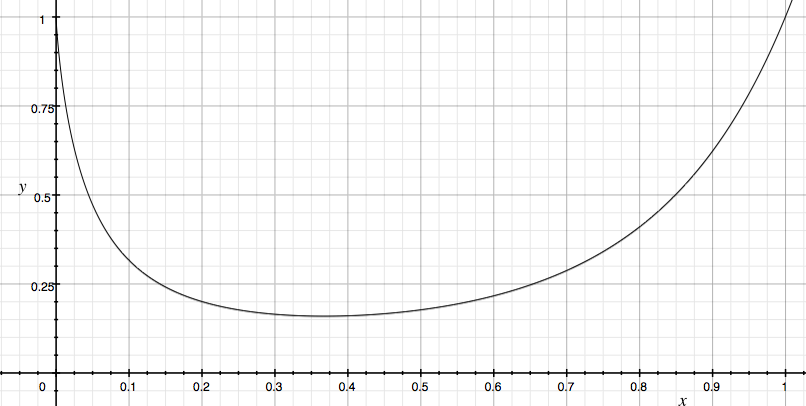
(3*x)cos produces a lovely curve, and its absolute value is ideal for scaling and offsetting (sound example D 1) Quad Amp Non-Linear Panning):

     

x ** (5x) produces a truly non-linear curve that never reaches zero (sound example D 2) Quad Amp Non-Linear Panning)

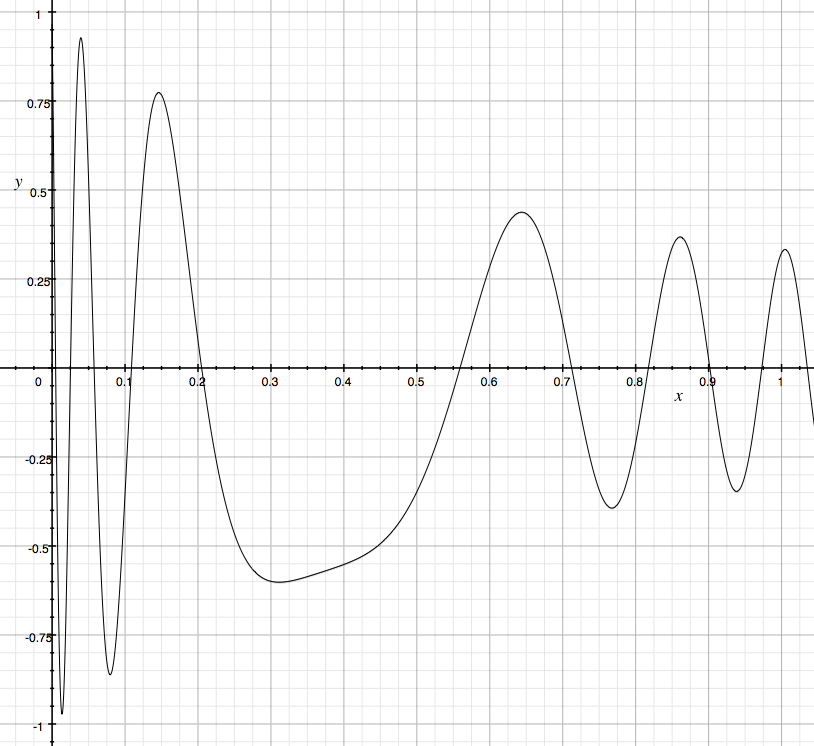
And my favorite, in terms of how it looks on the page, (1÷(2x+1))*cos*(50*(x**x)). My attempt at realizing this (sound example D 3) Quad Amp Non-Linear Panning) hasn’t quite panned out (pun intended). It results in very linear behavior, so there may be a point of diminishing returns.

Now, I want to return to the metaphoric model of the mobile or the orrery. These algorithms program the behavior of a sound to respond to changes of amplitude by modifying its apparent location in space. The path it takes is represented by the curves, mapped to the multichannel location of speakers. If I visualize each sound as one of the individual objects in the Calder mobile, then the algorithms determining panning are equivalent to the wires connecting each object in the mobile to each other. This is a form of structural coupling. All of the objects in Calder’s mobile are coupled to each other, some directly, others indirectly. They’re all structurally coupled to the environment, by the wire connected to the ceiling and the movement of air in the hallway.

In addition to providing a means of visualizing one approach to ecosystemic programming, this metaphor also provides a path for aesthetic evaluation of ecosystemic art. It suggests a musical work that does not have a defined beginning, middle, and ending, but one that is entered into. It also suggests Lev Manovich’s notion of new media as artwork that can be navigated by the audience. Much as I navigated the environment at the Hirschhorn when I encountered Calder’s mobile in order to change my perspective and engage with the piece from various vantage points, performers and audience alike can navigate the space of an ecosystemic work. The navigation can be perceptual or, if allowed, physical.

Part 3 will address ecosystemic control of timbral/spectral components.