Thoughts on FM: behind the algorithms

In the past, the Frequency Modulation technique was used widely in radio transmission but had not been applied to sound synthesis. In the early 1970s, John Chowning, a composer and researcher at Stanford University, developed some important new techniques for music synthesis using FM: the FM algorithms. In the late 70’s I found myself exploring FM techniques on the ARP 2600 the analogue way. By using spring reverberation between the modulator and carrier, blurring the spectrum, I found FM an extremely useful technique for creating impressive sonic structures. The aim of this writing is to find useful extensions of the FM technique in Kyma. The sine wave oscillators in these sounds are called “Operators”, OP(n) in short, like in the algorithms of Yamaha’s DX7. In these articles, the focus will be on the more practical side of FM synthesis and extensional techniques.

You can find all of the Kyma Sounds used here in the FM Tutorial archive in the Community Library.

The technical story behind the FM

Simply put, FM involves two sine waves. One is called the modulating wave, the other the carrier wave. The modulating wave changes the frequency of the carrier wave. It can be easiest to visualize, understand, and hear when the modulator is low frequency. (Open the file FM Basic 1.kym found in the FM Basic folder and play the Sound).

When set on a sine wave, the LFO modulation creates a vibrato. When the speed of this modulation is raised to within the audio spectrum, sidebands are obtained. These are complex harmonic structures (sound characters). These structures are defined by the ratio: the equation of pitch between the modulator and carrier. The number of harmonics that make a significant contribution to the spectrum depends on the modulation index. (Open FM Basic 2.kym).

FM sidebands:

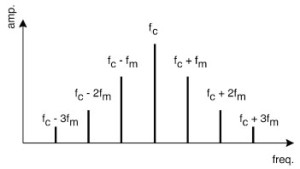
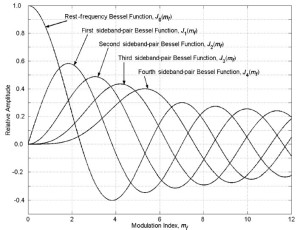
The FM spectrum can be considered to be made up of a carrier frequency at fc and an infinite number of sidebands at frequencies fc ± n*fm. The relative amplitude of a particular sideband at fc ± n*fm is governed by Jn(I), the Bessel function for the particular n.

The use of FM equations of an operator can be combined with one or more FM operators to synthesize different types of complex waveforms. In our first sound FM Basic 1 we can explore these functions in pitch ratio and amplitude. If we are experiencing the changes of timbre, when moving the sliders, we can imagine what would happen shaping these complex spectra:

Ratio: 1/1 creates a sawtooth wave.
Ratio: 1/2 creates a filtered square wave.
Ratio: 1/3 creates a 33% pulse wave.
Ratio: 1/4 creates a square wave, and so on.

How do we build in control of frequencies and amplitudes?

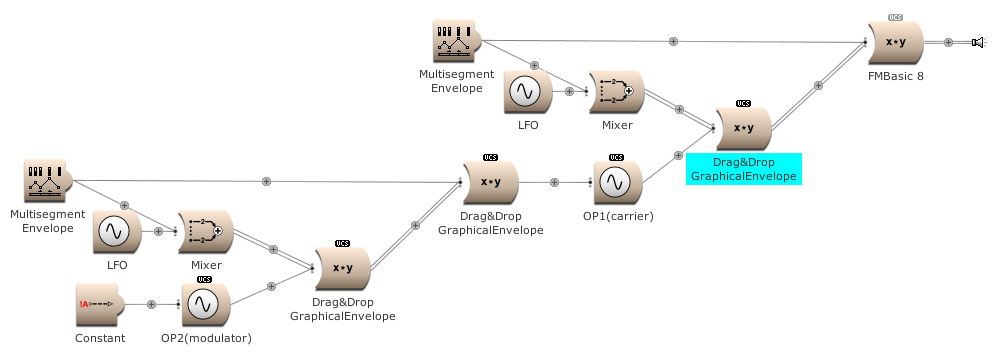
We have to create amplitude modulations. The product of the LFO’s sine wave and OP2 modulates the OP1’s frequency. The modulation of the LFO is increasing and decreasing the output of OP2. Therefore it sounds like a filter is opened and closed slowly. (Open FM Basic 3.kym).

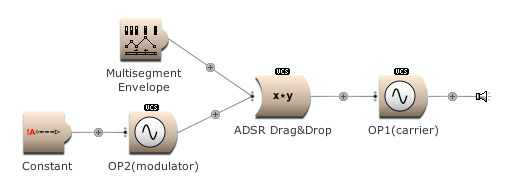
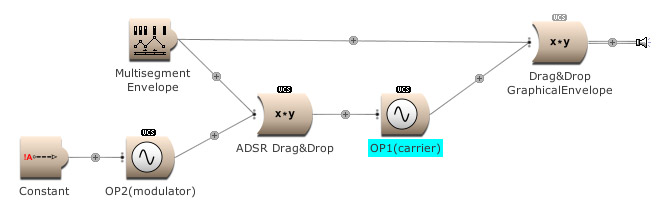
What happens if a Multisegment Envelope is used for modulating OP2’s output? Press the On button in the VCS. (Open FM Basic 4.kym).

The timbre modulation is as recognizable as an EG [envelope generator] modulation on a LP [low pass] filter. The output of the carrier OP1 was constant amplitude. We can start and modulate it’s amplitude with the same EG as from OP2, the modulator. Press the On button to hear it. (Open FM Basic 5.kym).

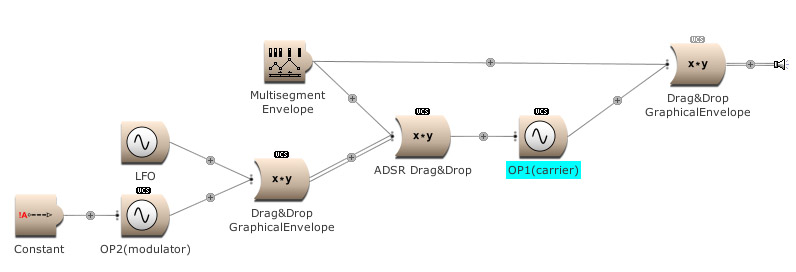
We even can add the LFO, from the first amplitude modulation example, and EG energy level to modulate the input of OP1. Press the On button again. (Open FM Basic 6.kym).

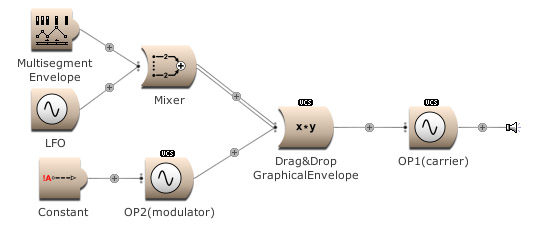
In the next example a Mixer module is used to add the outputs from the Multisegment Envelope and LFO to modulate the FM index. Try the On button. (Open FM Basic 7.kym).

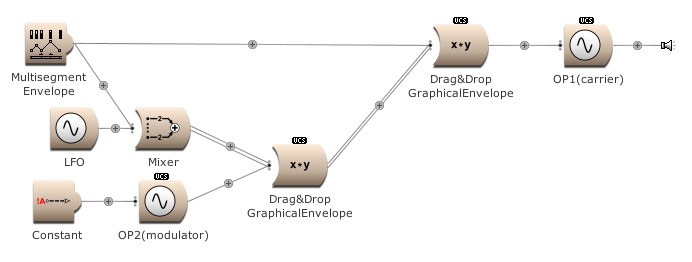
How can an EG, the Multisegment Envelope, control the amount of modulation of the EG itself and the LFO? Press On. (Open FM Basic 8.kym).

Adding things together. For both, carrier and modulator, available amplitude modulators. Press the On button again to hear. (Open FM Basic 9.kym).

The !On can be replaced by the expression !KeyDown to use a keyboard.

A word on Feedback in the algorithms

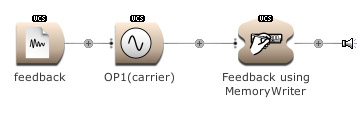
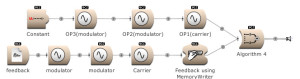
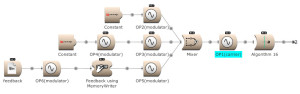
Equations, amplitudes and ratios are creating spectra. But what about creating noise? By routing back a signal to itself we can create noise and is called feedback. For this, the use of a MemoryWriter module is necessary [or by using a FeedbackLoopInput and FeedbackLoopOutput pair]. The information, written into the memory location, is read by the Sample player module. Check the box for FromMemoryWriter in the Sample module. (Open FM Basic 10.kym).

Connections in the Algorithm

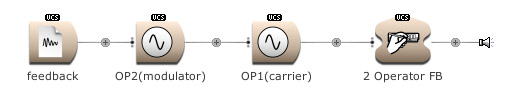
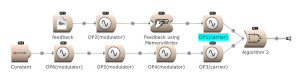
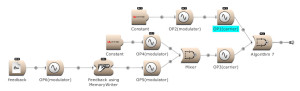
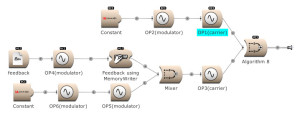
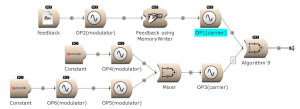
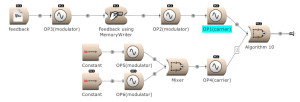
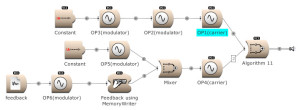
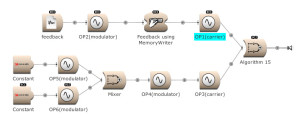
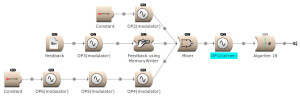
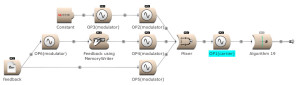
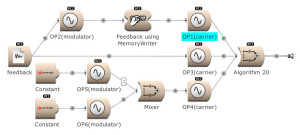
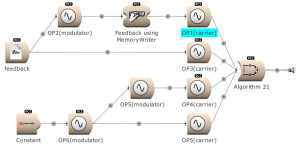
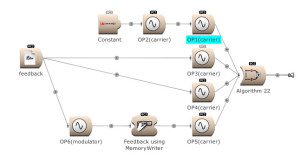
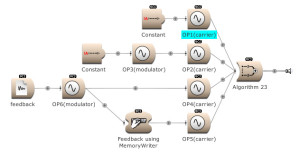
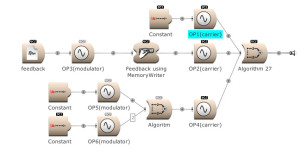
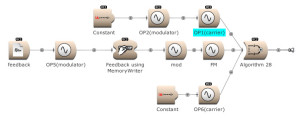
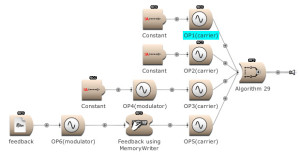
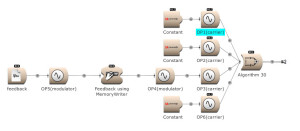
Feedback can be used over several operators. Here OP2 modulates OP1. The output of OP1 is written into the memory [for feedback] and is modulating OP2. (Open FM Basic 11.kym).

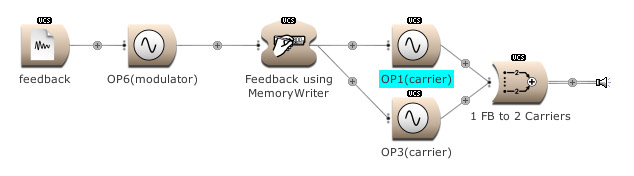
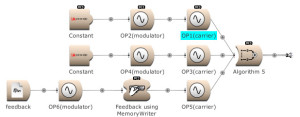
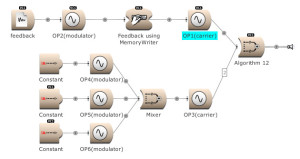
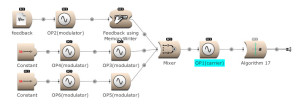
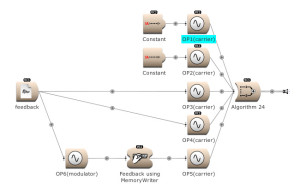
The modulator’s output, and feedback, can be used to modulate several Operators. (Open FM Basic 12.kym).

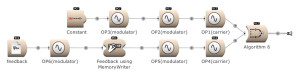
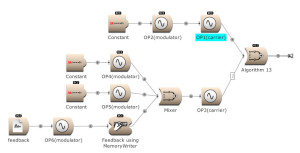
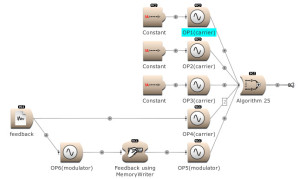
The feedback output is used directly on Operator 1 and indirectly (via Operator 4) on Operator 3. (Open FM Basic 13.kym).

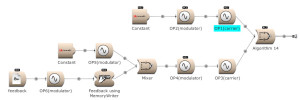
A sine wave combined with noise. (Open FM Basic 14.kym).

I hope you have enjoyed Part I.

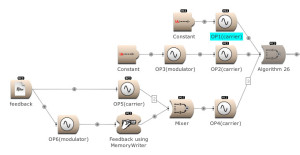
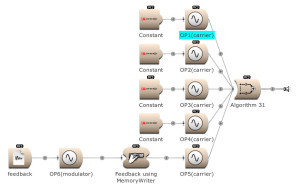
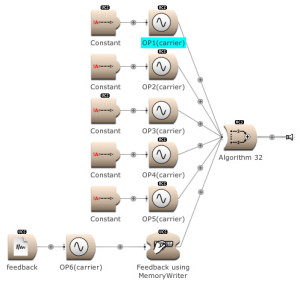
Below, and in the archive in the Community Library, I have included the 32 DX7 algorithms as a kind of ‘static Sound photo album’, without any amplitude modulations other than the amplitude faders of the Indexes. In my next article there will be more exploration of these algorithms…

32 algorithms: