How do Splines work in the InputOutputCharactersitc Sound?

Question

I'm trying to make a simple, variable transforming function from an InputOutputCharacteristic.

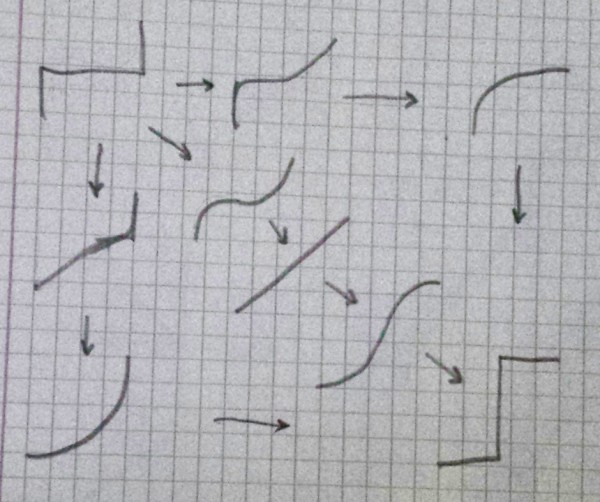
I want it to go from a simple curve above y=x (eg.y=x**1/2), through linear (y=x) to a curve below (eg. y=x**2).

I also want it to go from an "S" curve (one that goes horizontal, vertical, horizontal) to a rotated/reflected "S" curve (one that goes vertical, horizontal, vertical).

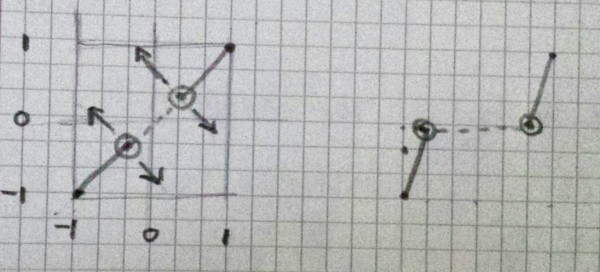
I'm doing this by having two Input / Output points that I move and then use Smoothing to spline between them.

 

Here's the code...

InValues: -1.0 {!Bottom - 1} !Top 1.0
OutValues: -1.0 {!Bottom negated} {1 - !Top} 1.0

So I'm achoring the start of the curve at (-1, -1) and the end of the curve at (1, 1).

The "Bottom" point moves along a line from (-1, 0) to (0, -1).

The "Top" point moves from (0, 1) to (1, 0).

If I set Smoothing to 0.5, ie. linear, I get a 3 segment linear curve that does excatly what I'd expect. But when I try smoothing it, it goes asymetric. For instance for curves above y=x the smoothed curve leaves the Bottom point smoothly but overshoots and joins the Top point at a discontinuity.

How do I get the curve symmetric, especially when the bottom section is near vertical and the top section near horizontal (or vice versa)?

 

 

Comments

I've done a bit of a fudge which helps but doesn't make properly symmetric curves:

In the Smoothing parameter I put:

((1 - (1 - (!Slope * 2)) abs) ** (2 + ((!Slope lt: 0.5) * (!Opposite + 1)) ) ) / 2 + 0.5

Where !Slope is the main control that sweeps through different curves. At 0.5 the curve is a straight line ramping from (-1, -1) to (1, 1). As !Slope decreases it tends towards a curve above y=x. As !Slope increases it tends towards a curve below y=x.

!Opposite changes the direction of the movement of the Top point in order to make "S" curves.

The expression above makes Smoothing vary from 0.5 (linear) to 1 (fully smoothed). For different shaped curves it makes Smoothing vary with !Slope to the 2nd, 3rd or 4th power.