How might one morph between n > 4 sounds scattered across a 2D plane?

Question

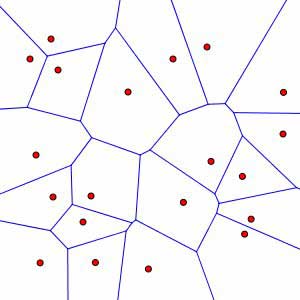
Hi, I'm interested in exploring a possible approach to sound morphing, where the output of an external machine-learning algorithm (a Kohonen self-organizing map) might resemble something like the diagram below, where each digital audio file in the input set ends up as one of the red dots below. Any of the neighboring sounds/dots to any selected sound/dot will have a higher likelihood of similarity to the selected item, according to the chosen feature metrics used to analyze the set of sounds. 

I've encountered a 2D morphing example in Kyma, where each of four sounds are placed in each of the four corners of a square, enabling a real time morph between all four sounds to be controllable via an XY-pad or any set of two controllers.

My question is:

Using Kyma, in order for a morphing process to accommodate an input set of sounds whose 2D similarity representation can be viewed as a Voronoi diagram like shown below...

(a) would it make the most sense to choose a quadrilateral of the four closest points to any point (where one of the points is the identified/selected point), and then treat those four points as the four points of the regular 2D morphing square (with or without a 2D transform to inverse skew the particular 4-sided shape into a square). The choice of quadrilateral would need to be selected separately, via a tablet for example.

(b) or is-there / might-there-be a way to morph between more than four sounds at once, as long as a weight value was provided for each sound, with all weights adding up to 1.0

(c) what else am I missing?, or any comments/suggestions are eagerly welcomed

Thanks,

Thom

Comments

ad (b) Did you try the Morph3D class?

---

That could be a very useful solution, for morphing up to 8 sounds. I didn't make that connection before, but now it seems like a perfect solution. Thanks !

I was also stuck on what points to use as the center of valid morphs. The red dots wouldn't work well, since a sound exists there as well. After some googling, this seems like a good place to start:

 For any region in the diagram, a usable "center-point" might be found at any vertex, or alternately, at the midpoint of each side. From there, locate the closest red points surrounding the point.. this would have to be defined algorithmically.. (i.e. choose an existing solution).. looking at the example diagram above, there seems to be from 5 - 8 red dots neighboring around most vertices. Midpoints usually appear to require less neighbors than the vertices, since the axis perpendicular to any bisected side yields two immediate red-dot neighbors, one on each side and equidistant. Intuition or common-sense suggests that the vertices will likely work much better than the midpoints.

I think I need to learn more about the computational-geometric properties of Voronoi diagrams and related algorithms to really figure out what approach(es) would be best to try from a purely mathematical perspective. If it yields more than one approach, see which one sounds best for a given set/class of sounds. It's good to know that after deciding on some approach(es), they should work well with the Kyma 3D morph, up to a maximum of 8 sound inputs to the morphing process.

---

The above approach would still require the user to select a morphing region with a tablet. I'm realizing now that my initial interest in using this kind of approach was more straightforward..

I originally envisioned the whole 2D plane shown in the diagram to be accessible via an XY-controller, such that for any point chosen by the user on the 2D plane, the delivered sound is the result of a morph between the N surrounding neighboring sounds (where N <= 8, which we now know).  

Again, some investigating into the mathematical properties of Voronoi diagrams should likely help to arrive at a feasible solution.

Just offhand:

Each vertex could define a center-focal point of its surrounding N sound input neighbors, establishing a separate set of morphing inputs for each vertex (call this an "input-sound-region").

Then, depending on the 2D coords of the user selection, the closest input-sound-region is selected, using the midpoints of each side to demarcate the transitions between neighboring input-sound-regions. Once the user crosses the midpoint of some side, the corresponding neighboring input-sound-region now becomes the active input-sound-set to the morphing process.  

This intuitively seems correct, but I've already encountered some ambiguity when trying to imagine it working when looking at the above diagram (not to mention that there should really be a sound situated at each corner as well). Again, some learning should definitely help !

---

As a first approximation, perhaps you could try this (using InterpolateN or one of the Morph1D flavors):  Partition your graph into vertical slices or columns where the red dots are more or less in a straight vertical line within each column.  Assign an InterpolateN to each column (their control parameter would be the Y axis).  Then feed all the columns into a single InterpolateN whose parameter is the X axis.  Now the tricky part.  You would have to warp the !Interpolate controls in each Sound (using the Capytalk into: expression) according to how far off-axis each point is — how far it is askew from the strictly vertical X or horizontal Y.

---

This is exactly what I wanted to know.. Many Thanks !  I just now have seen your response for the first time, almost two months later after the response was posted.. I didn't know it was there.. I'll look more closely next time !  Thanks again, Thom